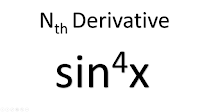Nth derivative of Sin^(4)x
In this quick tutorial you will learn that how to find the nth derivative of a trigonometric function like Sin(x) or Sin^4(x) by successive differentiation method. So observe each and every step very carefully and meanwhile if you have any doubt related to the solution at any step please leave us a comment we assure you that you will hear from us as soon as possible. So let’s now…..
Given: `y` = `sin^(4)x`
Multiply and divide `sin^(4)x` by 4 we get
`y` = `\frac{(2sin^(2)x)^(2)}{4}`
Or `y` = `\frac{(1-cos2x)^(2)}{4}` Since `(2sin^(2)x)^(2)=(1-cos2x)^(2)`
Now expanding `(1-cos2x)^(2)` we get the following result
i.e `y` = `\[\frac{(1 + \cos ^2 2x - \2cos 2x)}{4}\]`
Again, multiply and divide the term `(cos2x)^(2)` with 4 we get the following result.
i.e., `y` = `\[\frac{(1 + \frac{4\cos ^2 2x}{4} - \2.cos 2x)}{4}\]`
Or `y` = `\[\frac{1}{4} + \frac{1}{16} + \frac{1}{16}\(1+cos 4x)^2 - \frac{1}{2}\cos 2x\]`
Or `y` = `\[\frac{1}{4} + \frac{1}{16} + \frac{1}{16}\(1+cos^(2) 4x+2cos4x )- \frac{1}{2}\cos 2x\]`
Again Multiply & Divide `cos^(2)4x by 2 we get a result which is differentiable easily.
Or `y` = `\[\frac{1}{4} + \frac{1}{16} + \frac{1}{16}\(1+\frac{2cos^(2) 4x}{2}+2cos4x )- \frac{1}{2}\cos 2x\]`
Or `y` = `\[\frac{1}{4} + \frac{1}{16} + \frac{1}{16}\(1+\frac{1+cos8x}{2}+2cos4x )- \frac{1}{2}\cos 2x\]`
Or `y` = `\[\frac{1}{4} + \frac{1}{16} + \frac{1}{16}\1+\frac{1}{32}+\frac{cos8x}{32}+\frac{cos4x}{8} - \frac{1}{2}\cos 2x\]`
Now since `n_th` derivative of `sin(ax+b)` is:
= `[\a^(n). sin(ax+b+n.\frac{\pi }{2}]`
So, now writing `n_th` derivative of each term we get.
= `\frac{1}{32}\8^(n). sin(8x+n.\frac{\pi }{2})` - `\frac{1}{8}\4^(n). sin(4x+n.\frac{\pi }{2})` -
`\frac{1}{2}{.2^n}.\cos (2x + n.\frac{\pi }{2})`
No comments:
Post a Comment