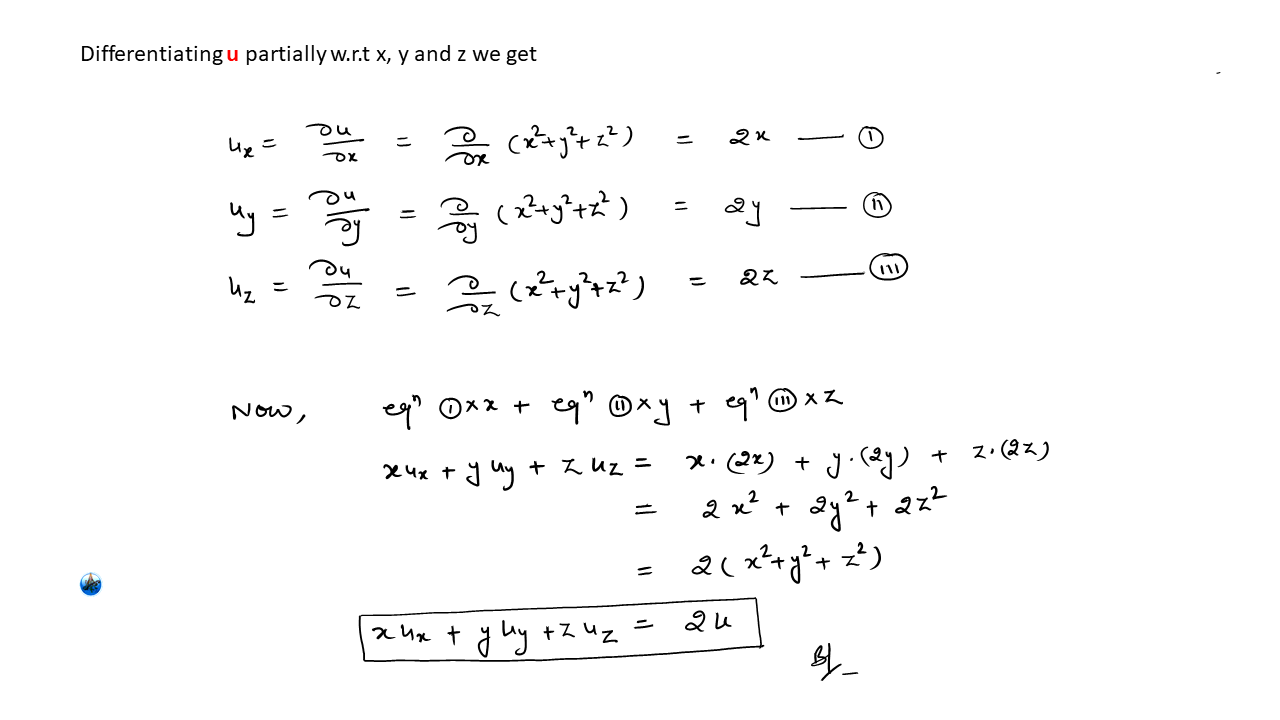Show That XUx + YUy + ZUz = 2U If U = X^2 + Y^2 + Z^2 | Partial Derivatives Solved Example

Show That XU_x + YU_y + ZU_z = 2U If U = X² + Y² + Z²

Solved example of partial derivatives with complete step-by-step explanation.

Given

U = X² + Y² + Z²

To Prove

XU_x + YU_y + ZU_z = 2U

Click or tap the image to view in full size.

Solution

Step 1: Partial derivative of U with respect to X

U = X² + Y² + Z²
∴ U_x = ∂U/∂X = 2X

Step 2: Partial derivative of U with respect to Y

U_y = ∂U/∂Y = 2Y

Step 3: Partial derivative of U with respect to Z

U_z = ∂U/∂Z = 2Z

Step 4: Substitute in XU_x + YU_y + ZU_z

= X(2X) + Y(2Y) + Z(2Z)

Step 5: Simplify

= 2(X² + Y² + Z²)
= 2U

Hence Proved

XU_x + YU_y + ZU_z = 2U ✔

Watch the full video solution below 👇

Related Mathematics Articles

• Integration by Partial Fractions
• Integration by Parts Examples
• Nth Derivative Using Leibnitz Rule

🎧 Best Study Earbuds

Boat Airdopes Joy Airdopes 219 (4 Mic) Airdopes 91 Prime Airdopes 131 Gen 2 Airdopes 101v2