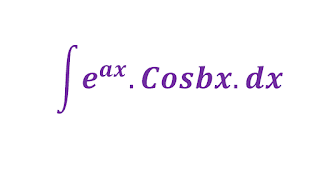Integration of e^ax cosbx || Integration by parts || important Integrals for competitive and board exams

                                       Chapter: Integration by parts

Q2. Find the integration of `\e^{ax}\cosbx`

Sol: Let ` I = \e^{ax}\cosbx`

From integration by parts method

`\1^{st}part\int {2^{nd}part - } \int {(\frac{d}{{dx}}} {1^{st}}part\int {{2^{nd}}partdx)dx} \]` …………………(1)

So, let `1^{st}part = \e^{ax}`        And        `2^{nd}part = cosbx`

Now put these values in eq (1) we get-

` I =\int\e^{ax}\cosbx`

 I = `e^{ax}\int \cos bx -- \int (\frac{d}{dx} e^{ax}\int \cos bxdx)dx `

 I =  ` \frac{1}{b}e^{ax}.\sinbx - \int a e^{ax}\frac{\sinbx}{b}dx`

 I =  `\frac{1}{b}e^{ax}.\sinbx - \frac{a}{b}[e^{ax}\int \sinbxdx  - \int (\frac{d}{dx} e^{ax}\int \sinbxdx)dx]`

 I =  ` \frac{1}{b}e^{ax}.\sinbx - \frac{a}{b}[-e^{ax}\frac{\cosbx}{b} + a\int {e^{ax}.\frac{\cosbx}{b}dx} ]`

I =  `\frac{1}{b}e^{ax}.\sinbx + \frac{a}{b^{2}}e^{ax}\cosbx` - `\frac{a^{2}}{b^{2}}\int e^{ax}.\cosbxdx `

 I =  `\frac{1}{b}e^{ax}.\sinbx + \frac{a}{b^{2}}e^{ax}\cosbx` - `\frac{a^{2}}{b^{2}}. I`

 I + `\frac{a^{2}}{b^{2}}.I`=   `\frac{1}{b}e^{ax}.\sinbx + \frac{a}{b^{2}}e^{ax}\cosbx`

   

  I.(`\frac{a^{2}+b^{2}}{b^{2}})` =  `e^{ax}. \frac{b.sinbx + a.cosbx}{b^{2}}`   

Or   I = `e^{ax}. [\frac{b.sinbx + a.cosbx}{a^{2}+b^{2}}]` 

Which is our final answer for the integration of `\e^{ax}\cosbx`

Similarly we will also find integration of  `\e^{ax}\sinbx` 

                                                                                   👉 integration of  `\e^{ax}\sin bx`