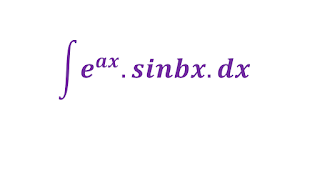Integration by parts || Integration of e^ax sinbx || Important Question from integrals

                     Chapter: Integration by parts

---

---

In this chapter we will learn two things very clearly.

1. what is 'Integration by parts' formula

2. we will also learn how to apply 'Integration by parts formula' into our questions to find their integrals with the help of this method.

We have taken an example to which best explains this method at the end of this question we will leave few questions for you so that you can practice this method more.

Q1. Find the integration of e^ax sinbx

Sol: Let ` I = \e^{ax}\sinbx`

From integration by parts method

`\1^{st}part\int {2^{nd}part - } \int {(\frac{d}{{dx}}} {1^{st}}part\int {{2^{nd}}partdx)dx} \]` …………………(1)

So, let `1^{st}part = \e^{ax}`        And        `2^{nd}part = sin bx`

Now put these values in eq (1) we get-

`I = \int\e^{ax}\sin bx`

 I = `e^{ax}\int \sin bx -- \int (\frac{d}{dx} e^{ax}\int \sin bxdx)dx `

 I =  `- \frac{1}{b}e^{ax}.\cos bx + \int a e^{ax}\frac{\cos bx}{b}dx`

 I =  `- \frac{1}{b}e^{ax}.\cos bx + \frac{a}{b}[e^{ax}\int \cos bxdx  - \int (\frac{d}{dx} e^{ax}\int \cos bxdx)dx]`

 I =  `- \frac{1}{b}e^{ax}.\cos bx + \frac{a}{b}[e^{ax}\frac{\sin bx}{b} - a\int {e^{ax}.\frac{\sin bx}{b}dx} ]`

I =  `- \frac{1}{b}e^{ax}.\cos bx + \frac{a}{b^{2}}e^{ax}\sin bx` - `\frac{a^{2}}{b^{2}}\int e^{ax}.\sin bxdx `

 I =  `- \frac{1}{b}e^{ax}.\cos bx + \frac{a}{b^{2}}e^{ax}\sin bx` - `\frac{a^{2}}{b^{2}}. I`

 I + `\frac{a^{2}}{b^{2}}.I`=   ` \frac{a}{b^{2}}e^{ax}\sin bx`- `\frac{1}{b}e^{ax}.cos bx`   

  I.(`\frac{a^{2}+b^{2}}{b^{2}})` =  `e^{ax}. \frac{a.\sin bx- .b.cos bx}{b^{2}}`   

Or   I = `e^{ax}. [\frac{a.\sin bx- .b.cos bx}{a^{2}+b^{2}}]` 

Which is our final answer for the integration of `\e^{ax}\sin bx` 

Similarly we will also find integration of `\e^{ax}\cos bx`

                                                           👉integration of `\e^{ax}\cos bx`